Familias de poliedros

Se presentan algunos de los tipos de poliedros que existen, de forma breve e introductoria. Se realiza además una clasificación y descripción básica, así como el proceso de formación. Se recomienda acceder a los enlaces para visualizar los poliedros. (Actualización)

Sólidos platónicos: Son los más conocidos y los únicos regulares y convexos a la vez. Existen cinco: Tetraedro (existe un interesante artículo dedicado al tetraedro publicado recientemeente en gaussianos), Cubo, Octaedro, Dodecaedro y Icosaedro.
Los demás sólidos se generan a partir de estos.

Sólidos de Kepler-Poinsot: Son también regulares pero cóncavos. Se logran a partir de adiciones sobre las caras de los sólidos platónicos. Existen cuatro: pequeño dodecaedro estrellado (imagen), gran dodecaedro estrellado, gran icosaedro y gran dodecaedro.

Sólidos arquimedianos: Son poliedros convexos de caras regulares y vértices uniformes pero no de caras uniformes. Se obtienen truncando (cortando por los vértices) los sólidos platónicos. El truncamiento se suele hacer a 1/3 de las aristas. Son simétricos salvo el Snub cube.

Son 11: tetraedro truncado, cuboctaedro, cubo truncado(imagen L), octaedro truncado, rombicuboctaedro, cuboctaedro truncado, icosidodecaedro(imagen R), dodecaedro truncado, icosaedro truncado, rombicosidodecaedro y icosidodecaedro truncado.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

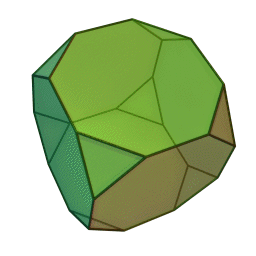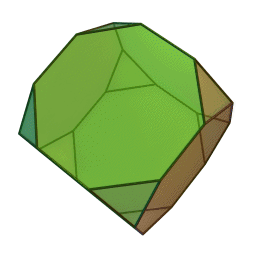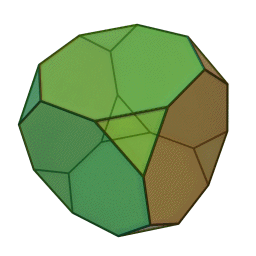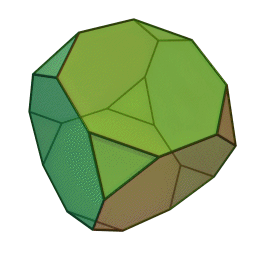
Existen otros como el cubo romo o el dodecaedro romo.

Sólidos duales: Existen de dos tipos y para formarlos:
a) Se calculan los puntos medios de las caras de los sólidos platónicos (1) Se unen los puntos y se genera un nuevo sólido platónico. De modo que el número de caras del sólido original pasan a ser el número de vertices del sólido generado. Tras realizar estas operaciones en un:

• Tetraedro se genera otro tetraedro más pequeño, ya que tiene 4 caras y 4 vértices.
• Cubo (6 caras) se genera un octaedro (6 vértices)
• Octaedro (8 caras) se genera un cubo (8 vértices)
• Dodecaedro (12 caras) se genera un icosaedro (12 vértices)
• Icosaedro (20 caras) se genera un dodecaedro (20 vértices)

b) Se inscribe el sólido platónico en una esfera. Se realiza de nuevo (1), se calcula el centro del poliedro y luego los puntos de corte en la superficie de la esfera con la prolongación de la recta que pasa por el centro y cada punto medio de las caras. Se une cada punto de corte con los vértices de la cara que le corresponde. Se obtiene algo similar a los sólidos de Kepler pero con una determinada proporción.

Sólidos de Johnson: Son 92. La mayor parte de los poliedros de Johnson son derivados de los sólidos platónicos y de los arquimedianos agregando o quitando pedazos. En ocasiones se cogen dos polígonos regulares, por ejemplo dos cuadrados iguales, se sitúan a una cierta distancia paralelos, se gira uno de ellos , en este caso 45º, y se une cada uno de los vértices superiores con los dos que tiene debajo. Y Finalmente se añade en cada cara cuadrada una pirámide. Resultado: Han quedado sin tratar entre otros grupos los sólidos de Catalan o los deltaedros.

En Wolfam MathWorld podéis encontrar la mayor colección de poliedros en la red tratados uno a uno con aplicaciones java, plantillas, descargas, laboriosos cálculos, curiosidades...